Séance 5: Probabiltés

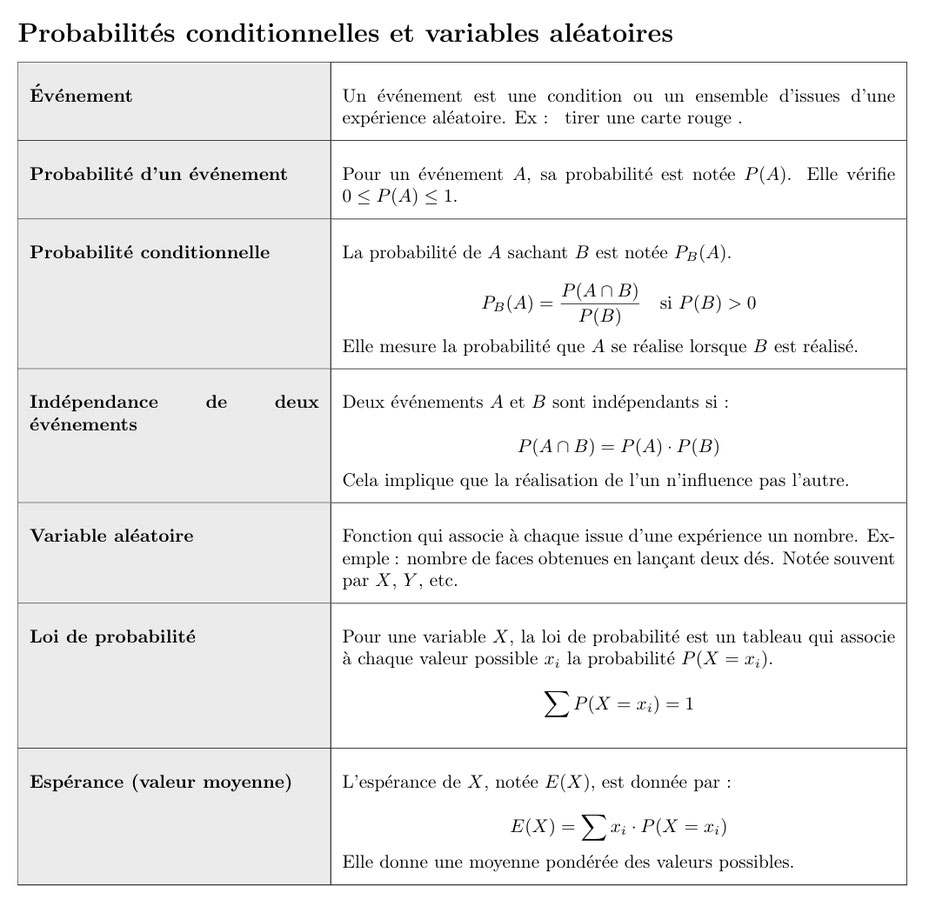
Partie 1: Probabilités

1. Dans une classe de 30 élèves, on a:
- 10 lycéens qui sont forts en maths;
- 12 qui aiment la physique;
- 7 qui aiment les deux matières.
On choisit un lycéen au hasard dans cette classe.
Déterminer la probabilité qu'il soit fort en maths sachant qu'il est fort en physique.

2. On tire au hasard une boule dans une urne contenant des boules noires et rouges indiscernables au toucher.
Cette urne contient 60% de boules noires.
Parmi les boules rouges, 75% sont gagnantes et parmi les boules noires, 25% sont gagnantes.
Calculer P(R∩G)?

3. On tire au hasard une boule dans une urne contenant des boules noires et rouges indiscernables au toucher.
Cette urne contient 60% de boules noires.
Parmi les boules rouges, 75% sont gagnantes et parmi les boules noires, 25% sont gagnantes.
Calculer P(G)?

4. On tire au hasard une boule dans une urne contenant des boules noires et rouges indiscernables au toucher.
Cette urne contient 60% de boules noires.
Parmi les boules rouges, 75% sont gagnantes et parmi les boules noires, 25% sont gagnantes.
Calculer P_G(R)?

5. Dans un jeu de 32 cartes, on tire au hasard une carte.
On note les événements:
- R: "on tire un roi";
- T: "on tire un trèfle".
Déterminer si les événements R et T sont indépendants?

6. On se place dans les mêmes conditions que dans la question 5, mais on ajoute deux cartes joker dans ce jeu de cartes.
Les événements R et T sont-ils indépendants?

7. On lance un dé cubique bien équilibré
On note:
- A:"obtenir un nombre pair"
- B:"obtenir un multiple de 3.
Les événements A et B sont-ils indépendants?

8. On tire au hasard une carte dans un jeu de 32 cartes.
On note:
- A est l’événement « la carte tirée est rouge »
- B est l’événement « la carte tirée est un cœur »
Les événements A et B sont-ils indépendants?

Partie 2: Mise en pratique

1. On lance trois fois de suite une pièce de monnaie.
On note X la variable aléatoire qui compte le nombre de "pile".
Déterminer les valeurs que X peut prendre?

2. On lance un dé non truqué à 6 faces.
- Si le résultat est pair, on gagne 2 euro;
- Si le résultat es supérieur ou égal à 5, on gagne 3 euros;
- Si le résultat est 1 ou 3, on perd 4 euros.
On note X la variable aléatoire donnant les gains à ce jeu.
Déterminer les valeurs de X?

3. On lance un dé non truqué à 6 faces.
- Si le résultat est pair, on gagne 2 euro;
- Si le résultat es supérieur ou égal à 5, on gagne 3 euros;
- Si le résultat est 1 ou 3, on perd 4 euros.
On note X la variable aléatoire donnant les gains à ce jeu.
Déterminer P(X=5)?

4. On tire une carte dans un jeu de 32 cares.
- Si on tire un as, on gagne 5 euros;
- Si on tire une carte noire, on gagne 3 euros;
- Si on tire une autre carte, on perd 1 euro.
On note X la variable aléatoire qui donne les gains à ce jeu.
Déterminer P(X=8)?

5. On lance deux dés non truqués.
On gagne 5 euros si on fait un double.
On perd 1 eurodans le cas contraire.
Quel gain moyen peut-on espérer?

6. Pour pouvoir jouer à un jeu, le joueur donne une mise de 1 euros.
Ensuite il lance un dé bien équilibré.
Il gagne 4 euros si le dé tombe sur 5 ou 6, il gagne 50 centimes si le dé tombe sur 2, 3 ou 4 et il perd 2 euros si le dé tombe sur 1.
Soit X la variable aléatoire qui donne le gain algébrique du joueur.
Déterminer les valeurs de X?

7. On se place dans les mêmes conditions que la question 6.
Déterminer l'espérance ?

8. On se place dans les mêmes conditions que les questions 6 et 7.
Ce jeu est-il favorable au concepteur du jeu?