Séance 4: Géométrie: Vecteurs

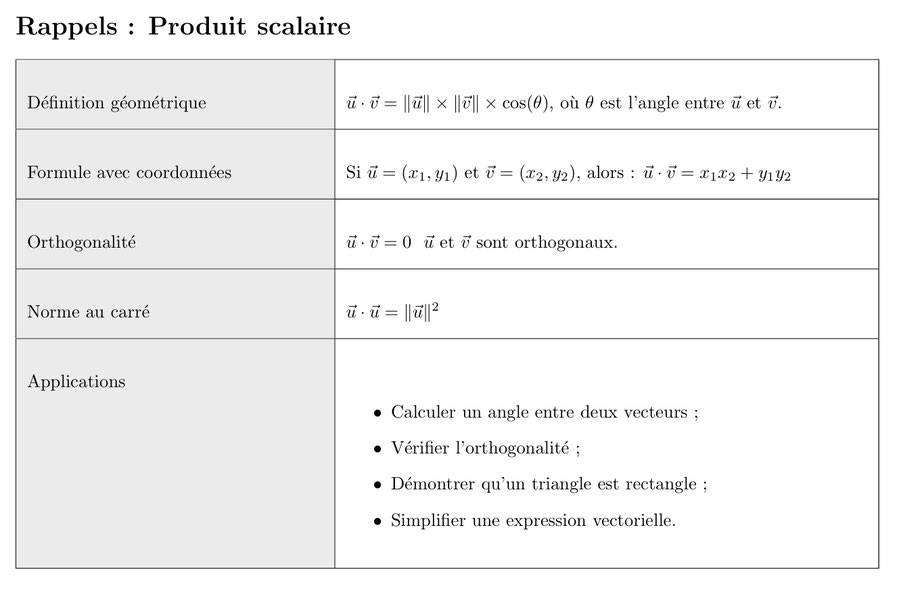
Partie 1 : Vecteurs, normes et produit scalaire

1. La relation de Chasles s'écrit :

2. Norme de → AB (3, 4) :

3. Si → AB(2, –1) et → BC(-1, 3), alors → AC

4. On considère les points A(1; 2) et O(0; 0).
Déterminer la distance OA?

5. On considère les points A(2; 1), B(6; 3) et C(3; 6).
Déterminer la valeur de cos(→ AB, → AC) et en déduire l'angle α = (→ AB, → AC) (on arrondira au degré près)

6. On considère ABC un triangle tel que: AB = 5cm, AC = 4cm et BC = 6cm.
Calculer → AB.→ BC.

7. On considère ABC un triangle tel que: AB = 5cm, AC = 4cm et BC = 6cm.
Calculer → BA.→ AC.

8. On considère ABCD un aprallélogramme tel que: AB = 4cm, AC = 6cm et (→ CD, → CA) = π/9.
Calculer → AB.→ AC.

Partie 2 : Colinéarité, Orthogonalité & Produit Scalaire

1. Deux vecteurs sont colinéaires si leur produit scalaire vaut zéro.
Vrai ou Faux ?

→ u(2; 3) et → v(4, 6) sont-ils colinéaires ?

3. Le produit scalaire de deux vecteurs orthogonaux vaut :

4. Dans un repère orthonormé (O; I, J), on donne: A(2; -1), B(4; 2), C(4; 0) et D(1; 2).
Les droites (AB) et (CD) sont ...

5. Dans un repère orthonormé (O; I, J), on donne: A(6; 0), B(4; 7) et C(-1; -2).
Le triangle ABC est ... ?

6. On considère ABCD un carré de côté 4cm et I est le milieu du segment [AB].
Calculer → AB.→ IC

7. On donne l'algoritrhme suivant:
Entrée:
Saisir a
Saisir b
Saisir c
Saisir d
Traitement: Si a.c + b.d = 0
Alors Afficher "Vrai"
Sinon Afficher "Faux"
Fin Si
Déterminer le rôle de cet algorithme?

8. On considère un segment [AB] et (d) sa médiatrice.
Elle coupe [AB] en K.
Soit M est un point de (d) différent de K;
On considère H le projeté orthogonal de K sur (AM).
Comparer → MK.→ BH et → MK.→ AH?