Cliquer sur la question pour obtenir la réponse
Second degré:
Qu'est ce qu'un polynôme du second degré?
Réponse:
Soient a,b et c trois réels tels que a≠0:
C'est une fonction de la forme: f(x)=ax²+bx+c.
Qu'est ce que la forme canonique?
Réponse:
Soit un polynôme du second degré: f(x)=ax²+bx+c
La forme: f(x)=a(x-α)²+β, où α=(-b)/(2a) et β=f(α) est appelée forme canonique
Dans les calculs, vous serez amené à utiliser l'une des trois formes:
1) La forme développée: f(x)=ax²+bx+c;
par exemple: pour calculer f(0).
2) La forme canonique: f(x)=a(x-α)²+β;
par exemple: pour calculer f(α).
3) La forme factorisée: f(x)=a(x-x1)(x-x2);
par exemple: pour calculer f(x)=0 (un produit de facteur est nul si l'un de ses facteurs est nul).
Comment déterminer la forme factorisée d'un polynôme du second degré?
Réponse:
Soit un polynôme du second degré: f(x)=ax²+bx+c
Trouver le discriminant: Δ=b²-4ac
1) Si Δ<0 , il n'y a pas de solution donc pas de factorisation.
2) Si Δ=0 il y a une solution x0=(-b)/(2a) et sa factorisation est: f(x)=a(x- x0)².
3) Si Δ>0, il y a deux solutions x1=(-b-√Δ)/(2a)
et x2=(-b-√Δ)/(2a)
La forme factorisée est: f(x)=a(x-x1)(x-x2).
Quel est le signe d'un polynôme du second degré?
Réponse:
P(x)=ax²+bx+c.C'est le signe de a SAUF entre les racines
1) Si Δ<0 :
| x | ∣ −∞ | +∞ | ||||
| ax²+bx+c | ∣ | signe de a |
2) Si Δ=0 :
| x | ∣ −∞ | x0 | +∞ | |||
| ax²+bx+c | ∣ | signe de a | 0 | signe de a |
3) Si Δ>0 :
| x | ∣ −∞ | x1 | x2 | +∞ | |||
| ax²+bx+c | ∣ | signe de a | 0 | -signe de a | 0 | signe de a |
Un polynôme du second degré est le produit de deux fonctions du 1er degré?
Réponse:
Vrai
(ax+b)(cx+d)=acx²+adx+bcx+bd=acx²+(ad+bc)x+bd
=Ax²+Bx+C=f(x), avec A=ac; B=ad+bc et C=bd
Si α est une racine d'un polynôme du second degré P défini par: P(x)=ax²+bx+c, que peut-on en déduire?
Réponse:
Si α est racine de P alors P(α)=0
On peut donc factoriser P par (x-α)
On obtient: P(x)=(x-α)(ax+b)
On développe et on identifie afin de trouver a et b.
Réponse:
Leur somme vaut:
Leur produit:
A retenir: Chercher deux nombres dont on connaît la somme s et le produit p revient à chercher les racines du polynômes:
Réponse:
On pose: X=x² et on obtient:
On calcule les racines X1 et X2, si elles existent (calculer le discriminant)
Puis on résoud X1=x²1 et X2=x²2
Attention: on peut obtenir entre 0 et 4 solutions!
Attention: Si X<0, alors x²<0: pas de solution (un carré est toujours positif).
Dérivation: Partie 1
Donner l'équation réduite d'une droite?
Réponse:
L'équation réduite d'une droite (non verticale) est de la forme:
y=mx+p, où m est le coefficient directeur et p l'ordonnée à l'origine.
Soient A(xA;yA) et B(xB;yB) deux points de la courbe représentative de la fonction f.
Déterminer le coefficient directeur de la droite (AB)
Réponse:
Le coefficient directeur de la droite (AB) est:
Soient A(a;f(a)) et B(a+h;f(a+h)) deux points de la courbe représentative de la fonction f.
Déterminer le coefficient directeur de la droite (AB)
Réponse:
Le coefficient directeur de la droite (AB) est:
On appelle ce nombre, (f(a+h)-f(a))/h, taux de variation de f en a ou taux d'accroissement entre A et B ou coefficient directeur de la droite (AB)
Soient A(a;f(a)) et B(a+h;f(a+h)) deux points de la courbe représentative de la fonction f.
Les points A et B sont très très proches.
Déterminer le coefficient directeur de la tangente au point d'abscisse x=a
Réponse:
Le coefficient directeur de la tangente au point d'abscisse x=a est:
On appelle ce nombre,f'(a), coefficient directeur de la tangente au point d'abscisse x=a.
Donner l'équation réduite d'une tangente au point d'abscisse x=a.
Réponse:
L'équation réduite d'une tangenteau point d'abscisse a est:
où f'(a) est le coefficient directeur et (f(a)-a.f'(a)) est l'ordonnée à l'origine.
Qu'est ce qu'une fonction f dérivable en x=a?
Réponse:
Une fonction f est dérivable en x=a, a réel:
On appelle L le nombre dérivé.
On dit que f est dérivable en a et f'(a)=L, L réel.
Dérivation: Partie 2
Qu'est ce qu'une fonction dérivée?
Réponse:
Soit f une fonction.
On appelle fonction dérivée de f, la fonction notée f' qui à tout x associe le nombre dérivé f'(x).
La dérivée sert à étudier les variations d'une fonction.
comment déterminer les variations d'une fonction f?
Réponse:
Soit f une fonction continue et dérivable sur un intervalle I:
2) Si f'(x)<0, alors f est décroissante sur I
3) Si f'(x)=0, alors f est constante sur I.
Qu'est ce qu'un extremum?
Réponse:
Un extremum peut être soit un maximum (M) soit un minimum (m).
On dit que:
2) Si f admet un minimum, alors f(x)≥m pour tout x
Comment déterminer si une fonction f dérivable sur un intervalle admet un extremum?
Réponse:
La fonction f est dérivable sur un intervalle I et soit a un réel appartenant à I (différent des bornes de I).
On dit que:
Attention: La réciproque est fausse:
Exemple: f(x)=x3 alors f'(0)=0 mais f n'admet pas d'extremum en 0 (f'(x)=3x²≥0, pas de changement de signe)
Le domaine de définition d'une fonction dérivée f' et le domaine de définition d'une fonction f sont identiques?
Réponse:
Faux.
Alors la fonction f est dérivable si et seulement si x>-2 et donc son domaine de dérivabilité est Df'=]-2;+∞[
Soient f et g deux fonctions.
Comment déterminer la position de ces deux courbes?
Réponse:
Etudier la position de deux courbes, c'est déterminer sur quel intervalle l'une est située au-dessus de l'autre.
On dit que:
2) Si f(x)-g(x)<0, alors la courbe représentative de f est en-dessous de celle de g
3) Si f(x)-g(x)=0, alors la courbe représentative de f coupe celle de g (point d'intersection).
Si la fonction est croissante, quelle observation peut-on faire sur les tangentes?
Réponse:
Soit f une fonction croissante sur un intervalle I, alors on observe que toutes les tangentes à la courbe Cf ont un coefficient directeur positif.
De même, si f est une fonction décroissante sur un intervalle I, alors toutes les tangentes à la courbe Cf auraient un coefficient directeur négatif.
Une entreprise fabrique des composants électroniques.
Le bénéfice est égal à la recette moins les coûts de fabrication.
Comment savoir si cette entreprise réalise des bénéfices et quand celui-ci sera maximum?
Réponse:
On étudie les variations de la fonction B(x)=R(x)-C(x), où R fonction recette et C fonction coûts de fabrication.
On étudie le signe de la dérivée (on trouve la valeur x0 qui annule la dérivée: B'(x0)=0) puis on fait le tableau de variations (croissant puis décroissant).
On lit sur le tableau la valeur y0 (on calcule B(x0)=y0) qui correspond au maximum.
| x | | 0 | x0 | +∞ | ||
| B'(x) | | + | 0 | - | ||
| y0 | |||||
| B | | ↗ | ↘ | |||
Suites: Généralités
Quelle est la définition d'une suite?
Réponse:
Une suite associe à tout entier naturel n un nombre réel noté un.
Comment montrer la monotonie d'une suite?
Réponse:
On calcule: un+1-un pour tout n∈ℕ
1)un+1>un: la suite est strictement croissante
2)un+1<un: la suite est strictement décroissante
3)un+1=un: la suite est constante
Comment représenter graphiquement une suite définie par récurrence?
Réponse:
On calcule: les termes de proche en proche à partir du premier terme et un+1=f(un).
1) Construire la courbe représentant f;
2) Construire la courbe d'éuqation y=x;
3) Placer u0 sur l'axe des abscisses;
4) Construire son image u1;
5) La reporter sur l'axe des abscisses à l'aide de la droite d'équation x=y;
6) Procéder de la même façon pour construire u2, ... .
Comment peut-on définir une suite?
Réponse:
1) Suite explicite:
Une suite est définie de façon explicite lorsqu'on dispose d'une formule du type un=f(n) permettant de calculer chaque terme de la suite à partir de son rang.
Exemple:
un=2n+3, on peut calculer u100=2x100+3=203.
2) Suite récurrente:
Une suite est définie par une relation de récurrence lorsqu'on dispose d'une formule du type un+1=f(un) permettant de calculer chaque terme de la suite à partir du
terme précédent.
Exemple:
un+1=2un+n-1 et on donne u0=1 pour calculer u2 il faut calculer d'abord u1=2u0+0-1=1 et donc
u2=2u1+1-1=2.
Comment représenter graphiquement une suite de façon explicite?
Réponse:
La représentation graphique d'une suite(un) pour tout n∈ℕ dans un repère du plan, s'obtient en plaçant les points de coordonnées (n;un) lorsque n parcourt ℕ.
Comment représenter graphiquement une suite de façon explicite?
Réponse:
Soit (un) la suite définie explicitement par un=f(n), où f est une fonction définie sur ℝ+, alors (un) a le même sens de variation que f:
1) si f est croissante, alors la suite (un) est croissante,
2) si f est décroissante, alors la suite (un) est décroissante.
Suites: Arithmétiques et Géométriques
Qu'est ce qu'une suite arithmétique?
Réponse:
Chaque terme est obtenu en ajoutant une constante r au terme précédent:
Comment montrer qu'une suite n'est pas arithmétique?
Réponse:
On utilise un contre-exemple:
u2-u1≠u1-u0
Quelle est la forme explicite d'une suite arithmétique?
Réponse:
Si (un) est une suite arithmétique de raison r, alors pour les entiers naturels n et p, on a:
Comment déterminer le nombre de termes d'une suite arithmétique ou géométrique?
Réponse:
p<n:
up, up+1, ..., un-1, un :
dernier indice-premier indice+1=n-p+1 est le nombre de termes.
Qu'est ce qu'une suite géométrique?
Réponse:
Une suite géométrique est une suite de nombres où chaque terme est obtenu en multipliant le terme précédent par une constante q appelée raison:
Comment montrer qu'une suite n'est pas géométrique?
Réponse:
On utilise un contre-exemple:
u2/u1≠u1/u0
Quelle est la forme explicite d'une suite géométrique?
Réponse:
Si (un) est une suite arithmétique de raison q, alors pour les entiers naturels n et p, on a:
Comment calculer la somme des n premiers termes d'une suite géométrique de raison q (q≠1)?
Réponse:
S=u0+u1+ ... +un
S=(1er terme).(1-qnombre de termes)/(1-q)
Trigonométrie:
Qu'est ce que le cercle trigonométrique?
Réponse:
C'est le cercle de centre O et de rayon R=1 sur lequel on a choisi comme sens positif le sens contraire des aigulles d'une montre (on dit aussi "sens direct").
Qu'est ce que la mesure principale d'un angle?
Réponse:
Sur le cercle trigonométrique, un point peut être associé à plusieurs valeurs.
La mesure principale d'un angle correspond à sa mesure qui est comprise dans l'intervalle ]-π;π].
Qu'est ce que les valeurs remarquables?
Réponse:
c'est le tableau qui donne les valeurs de "cosinus" et "sinus" pour les angles suivants:
0; π/2; π/3; π/4; π/6 et π
Qu'est ce que la périodicité d'une fonction et quelles sont les conséquences graphique pour la représentation graphique de la fonction f?
Réponse:
Si f(x+T)=f(x) on dit que f est périodique de période T.
En règle général la période d'une fonction est la plus petite période positive de cette fonction (si T est la période alors 2T l'est aussi)
Donc on fait l'étude sur un intervalle de longueur T et on répète le motif pour obetnir la courbe sur l'intervalle souhaité.
Exemples:
l) La fonction "cos" est 2π-périodique (car cos(x+2π)=cos(x)), donc on fait l'étude sur un intervalle de longueur 2π et on répète le motif pour obtenir la courbe sur
ℝ.
2) La fonction "sin" est 2π-périodique (car sin(x+2π)=sin(x)), donc on fait l'étude sur un intervalle de longueur 2π et on répète le motif pour obtenir la courbe sur
ℝ.
Qu'est ce que le radian et quel est son lien avec les dégrés?
Réponse:
Le radian est une unité d'angles.
1 π rad correspond à 180°.
Soit M un point sur le cercle trigonométrique associé au nombre réel x:
Le "cosinus(x)" et le "sinus(x)" correspondent à ?
Réponse:
Le cosinus de x, noté cos(x) et le sinus de x, noté sin(x) sont respectivement l’abscisse et l’ordonnée de M .
Qu'est ce que la parité d'une fonction et quelles sont les conséquences graphique pour la représentation graphique de la fonction f?
Réponse:
1) Si f(x)=f(-x) on dit que f est paire et sa courbe est symétrique par rapport à l'axe des ordonnées (= symétrie axiale, l'axe des ordonnées):
Exemple: la fonction "cos" est paire, donc sa courbe représentative est symétrique par rapport à l'axe des ordonnées.
2) Si f(x)=-f(-x) on dit que f est impaire et sa courbe est symétrique par rapport à l'origine du repère (= symétrie centrale de centre O)):
Exemple: la fonction "sin" est impaire, donc sa courbe représentative est symétrique par rapport à l'origine.
Comment résoudre les équations trigonométriques?
Réponse:
1) cos(a)=cos(b) équivaut alors à: a=b+2kπ où k∈ℤ ou a=-b+2kπ où k∈ℤ;
1) sin(a)=sin(b) équivaut alors à: a=b+2kπ où k∈ℤ ou a=π-b+2kπ où k∈ℤ
Exponentielles:
Qu'est ce que la fonction exponentielle?
Réponse:
C'est l'unique fonction dérivable sur ℝ vérifiant f'(x)=f(x) et f(0)=1.
Elle est notée: x⟼ex (ou exp(x))
Quelles sont les propriétés qui caractérisent la fonction exponentielle?
Réponse:
1) La fonction exponentielle est strictement positive sur ℝ.
2) La fonction exponentielle est strictement croissante sur ℝ.
Soit f(x)=ex, définie sur ℝ.
Quel est le résultat du produit: f(x).f(-x)=?
Réponse:
f(x).f(-x)=ex.e-x=ex-x
f(x).f(-x)=e0=1
Quels que soient les réels x et y, comment comparer ex et ey?
Réponse:
1) ex=ey équivaut à x=y;
2) ex≥ey équivaut à x≥y;
3) ex≤ey équivaut à x≤y.
(On a les mêmes résultats si les inéquations sont au sens strict)
Soit u(x) une fonction définie et dérivable sur un intervalle I, on donne f(x)=eu(x) alors que vaut f'(x)=?
Réponse:
f'(x)=u'(x).eu(x)
Exemple: Si u(x)=ax+b alors u'(x)=a et donc f'(x)=a.eax+b.
Comment simplifier l'expression suivante:
Réponse:
ea+h+ea+k=ea.eh+ea.ek=ea(eh+ek).
On factorise par ea
Comment simplifier une dérivée faisant intervenir ex?
Réponse:
1) Reconnaître la forme de la fonction à dériver (u+v; u.v; u/v; eu);
2) On utilise le fait que la dérivée de ex est elle-même;
3) On factorise, si possible, par ex le résultat afin d'étudier le signe du facteur restant (car ex>0).
Donner un exemple concret d'application des exponentielles dans un domaine scientifique ou économique.
Réponse:
Les exponentielles modélisent la croissance d’une population ou la décroissance radioactive.
Probabilités conditionnelles:
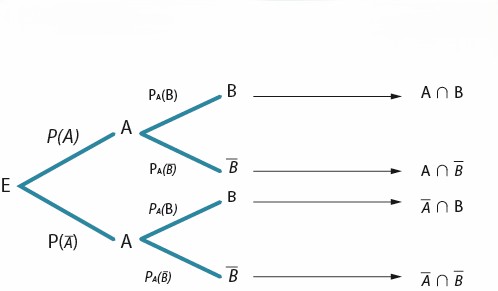
Qu'est-ce qu'une probabilité conditionnelle ?
Réponse:
La probabilité conditionnelle d'un événement B sachant que A est réalisé est notée PA(B) et se calcule avec la formule :
À quoi sert la formule des probabilités totales ?
Réponse:
Elle permet de calculer la probabilité d'un événement B en faisant la somme de tous les chemins A∩B et ̅A∩B qui y ménent.
B un événement de l'univers E et A et ̅A forment une partition de E. Alors, on a:
Soient A et B deux événements tels que P(A)≠0.
On note ̅B l'événement contraire de B.
Quelles sont les propriétés qui lient PA(B) et PA(̅B)?
Réponse:
Comment obtenir la probabilité de l'événement A∩B?
Réponse:
Calculer la probabilité d'une issue finale revient à multiplier les probabilités des branches qui y ménent.
Deux événements sont indépendants si… ?
Réponse:
Deux événements de probabilités non nulles sont indépendants si la réalisation de l'un n'influe pas sur la réalisation de l'autre.
Soient A et B deux événements de probabilités non nulles, ces deux événements sont indépendants si ...?
Réponse:
L'une de ces trois égalités est vérifiée:
Variables aléatoires:
Qu'est-ce qu'une variable aléatoire?
Réponse:
Une variable aléatoire associe une valeur numérique à chaque issue d’une expérience aléatoire.
A partir du tableau de la loi de probabilité, comment calculer P(X≤k)?
Réponse:
On utilise le tableau lié à la loi de probabilité suivie par X: on somme les probabilités des valeurs possibles jusqu'à k.
Dans un jeu d'argent, que signifie une espérance positive ou nulle
Réponse:
Si E(X)=0 alors le jeu est équitable.
Si E(x)>0 alors le jeu est favorable au joueur.
Que représente la variance?
Réponse:
La variance V(X) quantifie l’écart entre les valeurs de la variable et l’espérance.
Plus la variance est grande, plus les valeurs sont éloignées de l’espérance.
Cas particulier: si la variance est nulle, cela signifie que toutes les valeurs sont égales à l’espérance.
Qu’est-ce qu’une loi de probabilité?
Réponse:
C’est un tableau qui associe à chaque valeur de la variable aléatoire sa probabilité.
|
|
|
|
|
|
|
|
|
|
|
|
Que représente l'espérance pour un jeu d'argent?
Réponse:
L'espérance mathématique d'un jeu représente le gain moyen qu'un joueur peut espérer obtenir par partie au bout d'un grand nombre d'épreuves.
Dans un jeu d'argent, que signifie une espérance négative?
Réponse:
Si E(x)<0 alors le jeu est défavorable au joueur.
Dans un jeu d'argent, comment interpréter l'écart-type?
Réponse:
Dans un jeu d'argent, la variance et l’écart-type sont des indicateurs essentiels pour évaluer le niveau de risque et la stabilité des gains ou pertes.
Plus l’écart-type est grand, plus il est probable que les gains soient éloignés de l’espérance.
️ Un petit écart-type indique des gains réguliers.
